【】在2023年10月刊《准双作用式理论问题研究》一文中,笔者推导了准双作用式的活塞位移公式,介绍了其在压缩机研究、设计中的应用,并提到了压缩机动力计算。本文在探讨压缩机动力计算程序之前,先具体谈谈构成压缩机活塞力成分之一——惯性力的问题。
1、惯性力概念发展简史
先简单谈谈传统的手工绘制动力曲线的计算方法。构成列的活塞力由气体力、惯性力、摩擦力三部分相加之和而形成。列的气体力图采用勃劳厄(brauer)法绘制;列的惯性力图通常采用托尔(tolle)法绘制,近似地绘制出一阶、二阶惯性力之和;列的摩擦力图是按经验法绘制,通常的做法是在向轴行程中认为是一不变的正值,而在向盖行程中则认为是一负的不变的值,在内、外止点时作一斜线修正。它的作用方向始终与活塞运动速度方向相反。这三种方法绘制的各自力图中,都面临着横坐标的转换,因为活塞式压缩机是曲柄连杆机构,将主运动的旋转运动通过连杆转换成活塞的上、下往复运动。各自的力图一般先采用“力-位移”坐标系,它们都是周期性的,主曲柄旋转一周360°时,活塞则经“外止点-内止点-外止点”这样一个循环。而列的活塞力图一般采用“力-曲柄转角”坐标系构成,包括后来的列的切向力图、列的法向力图、列的连杆力图、列的侧向力图,都是采用这样的坐标系来分析。所以说,对于横坐标由行程转化为曲柄旋转角的问题,教材上都给出了采用勃力克斯(brix)近似作图法,并给予了相应证明,这里不作展开论述。这就是传统的手工作图方法,而现在则直接采用经推导的公式将三种力图直接绘制成“力-曲柄转角”坐标系中。不过有些细节仍是近似的。例如,气体力经气的作用,在转折点处没有考虑现实中的脉动状态,惯性力图也仅考虑了一、二阶,对其后的三阶等没有考虑,而摩擦力图是最简单的简化过程,并且统计出的机械效率具体值也是一个经验值。虽然是这样但这些简化也是我们动力计算时作出的正确抉择。
惯性力是什么?历史上关于惯性力的争论由来已久,可追溯到三百年前左右。惯性力就是按达朗伯原理,将动力学问题转化成静力学问题的一种研究方法。这种力比较特殊,它没有明确的力的三要素概念,所以有些人认为是虚拟的,它实际上是以“-ma”形式出现。而更多的学者坚持认为它是一种真实的力,不然就无法解释高速旋转的机器,例如航空燃气涡轮叶片根部断裂现象。这些在压缩机上也有类似的现象,归根到底都是实际物体的内力与外力、相对与绝对的问题。
2、压缩机中惯性力的大小
据作者统计,在各种型式的压缩机中,构成某一列的活塞运动组件,其该列受到的往复惯性力的幅值占该列所受到的气体力的幅值百分比,约为7~40%,这是作者不完全的统计。它基于作者目前所了解到的各种国内的压缩机经作者近似比算的,实际反映了各型的设计者对惯性力的认识作出的设计。请读者应该注意的是,这里的活塞包括单作用式、双作用式的,而这里的惯性力的演算方法则是该篇文章所详细讨论的内容。

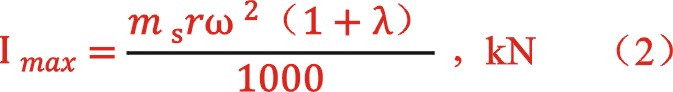
其中:imax——列的最大往复惯性力
ms——盖侧往复质量,包括盖侧活塞、环、活塞杆、十字头体、销、连杆重心偏向于小头部分的连杆质量(约占连杆总质量的30~40%),kg。轴侧质量待后面讨论
r——曲柄半径,m
ω——曲柄旋转角速度,1/s,,n为机器转速,r/min
λ——曲柄半径连杆中心距之比,,为连杆中心距长度

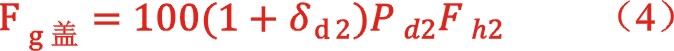
其中:δd2——准双作用式盖侧容积腔部分的排气时相对压力损失
pd2——准双作用式盖侧容积腔部分的名义的排气绝对压力,bar
fh2——该容积腔所作用的活塞面积,m2,

代表盖侧气缸直径

其中:p平——指平衡腔的压力,bar,它与机器的运动机构利用系数μ有关。一般接一级排压力腔,它可以减轻高压缸活塞环工作负荷,避免向低压级腔泄漏,这里计算b值时不考虑。
fh气缸圆环——指下面的大气缸与上面的小气缸工作面积差,m2
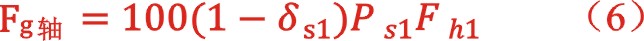
其中:δs1——准双作用式轴侧容积腔部分的吸气时相对压力损失
ps1——准双作用式轴侧容积腔部分的名义的吸气绝对压力,bar
fh1——该容积腔所作用的活塞面积,m2,
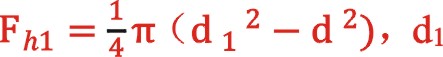
代表轴侧气缸直径,d代表活塞杆直径
pgas——列的最大气体力,它一般指的是盖侧活塞θ=0而轴侧活塞处在θ=π时的状态
b——惯性力的幅值与气体力的幅值的百分比,%
3、关于惯性力在准双作用式压缩机中表现形式的几种思考
大家知道,在曲柄连杆机构中,列的往复惯性力i为:
注意,它通常指的是盖侧活塞的惯性力。相信大部分读者可能都比较迷惑,为什么刚开始作惯性力图时,在外止点即θ=0时,将作在正力方向时,就能将上式“-”取消?这是因为,在盖侧活塞工作过程中,θ=0°开始后,位移由0渐变正(方向向下),速度也是由0渐变正(方向向下),而加速度则是由正的最大值渐变小(引起的速度还是渐变大),其方向也是向下,加个负号则方向变上,则此时该力的作用使连杆受拉,故手工作图时作在正力方向上,已考虑了“-”。
同理,θ=180°时,,该值为负,作在“力-曲柄转角”坐标系下方。
下面以具有图1形式的准双作用式压缩机某一列为算例,详尽讨论对变值的惯性力计算的思考。
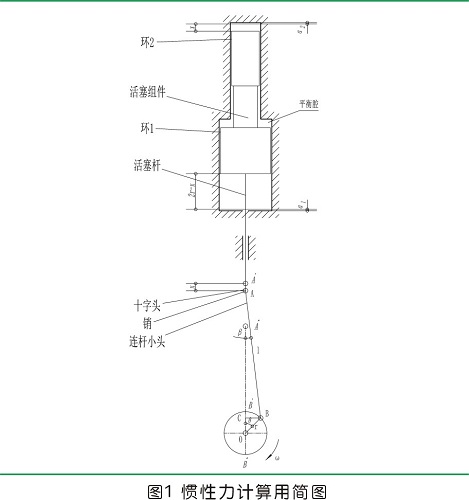
已知:活塞组件质量7.8kg(其上小活塞3.2kg,下面大活塞4.6kg)
环0.6kg
活塞杆8.2kg
十字头10kg
销1.4kg
连杆小头4kg
综上,运动部件总质量32kg,其中盖侧运动部件总质量27.4kg,轴侧运动部件总质量28.8kg
曲柄旋转半径

角速度
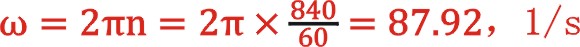
曲柄半径连杆比
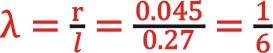
观点一:仅考虑了盖侧活塞组件的质量
由(7)式得到:
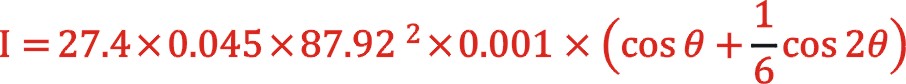
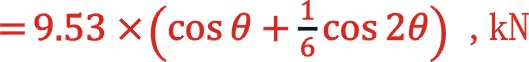
由此得到惯性力的最大值与最小值为11.13,-7.95kn。以该数系同气体力、摩擦力参与了该列活塞力的演算,忽略了轴侧大活塞的影响,可能当时还没有意识到轴侧惯性力如何计算。
观点二:因为按照动力的传递,由连杆小头带动十字头、活塞杆,进而大活塞、小活塞,作上下往复运动,认为:


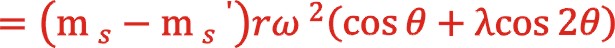
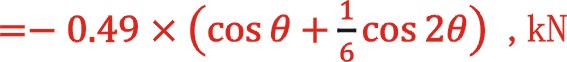
由此得到惯性力的最大值与最小值为0.41,-0.57kn。其中第二项是这样演算的:当将内止点选做坐标系的原点,向上为正方向,以轴侧活塞开始膨胀点为起始点后,其:
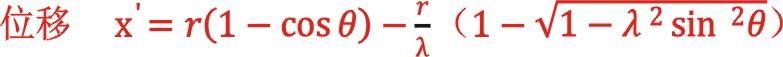

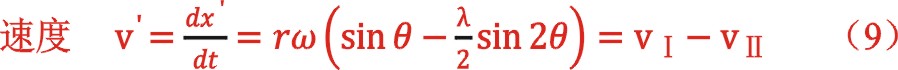
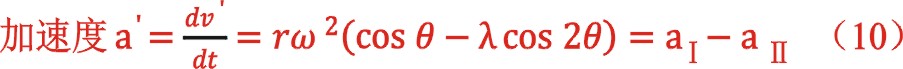
当盖侧与轴侧都统一到盖侧的外止点处一套坐标系后,也考虑到初始时各自的正负值后,总的惯性力应是盖侧的惯性力与式(10)的之和(不过后来发现还是不对),大家可能发现盖侧与轴侧往复质量中将连杆小头、十字头、活塞杆质量计及了两次,算出的参与计算的质量仅是大、小活塞质量的差值,这不知有没有道理?不过我们或许都知道,惯性力在机器运转过程中,不参与做功,不影响最终平均切向力的大小,仅影响活塞力和平均切向力的具体形状,影响机器曲轴的静强度计算,并且其幅值相对气体力来说较小。
观点三:由观点二得出推论, 、计入可能有误,应该是
、计入可能有误,应该是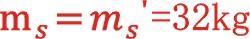 ,所以。
,所以。
观点四:不论以盖侧活塞计算惯性力的变化曲线,还是以轴侧活塞来计算,其计算结果都是一样的,即以观点一中的公式来计算,式中ms=32kg,证明如下:

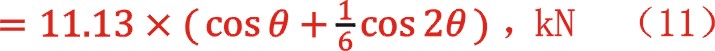
由此得到惯性力的最大值与最小值为13,-9.29kn。
根据盖侧的位移、速度、加速度图解,见图2。
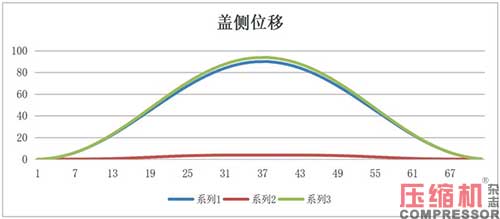
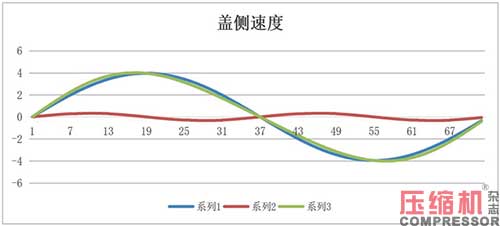
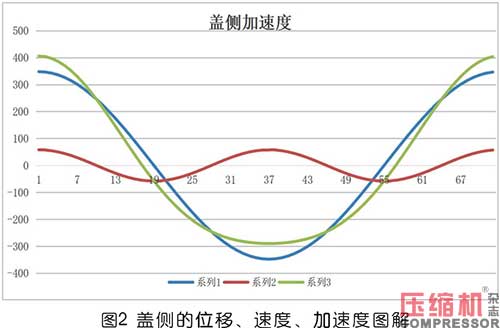
据轴侧的位移、速度、加速度图解,见图3。它就是按式(8)、(9)、(10)分两部分叠加而成。
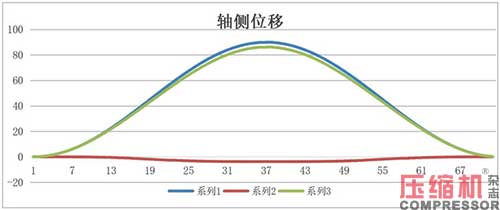
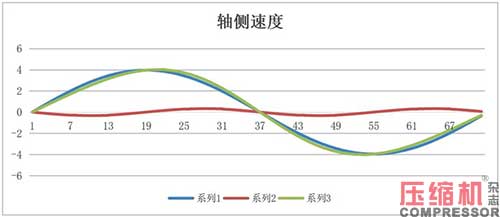
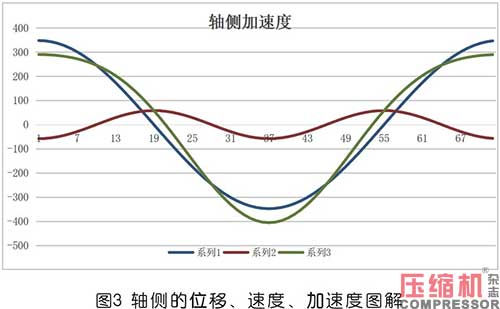
轴侧0°时,位移为正(方向向上),速度为正(向上),加速度为正(向上),-ma向下,连杆受压,作在负值(-1+λ)处;轴侧180°时,位移为正的最大值,速度为0渐变负(向下),加速度为负的最大值(向下),-ma向上,连杆受拉,作在正值(1+λ)处。
由此可见,形式上具有图1中的大活塞进行的轴侧加速度的变化,其受力分析表明,在统一的一套坐标系中θ=0时,将惯性力的起始点作在正的(1+λ)为力的系数处,参与的质量是全部的往复运动质量,这正好与普通盖侧惯性力曲线起始点作图一致。这很好地解决了观点二和观点三中十字头等处质量参与计算两次的问题,当时也因为这一处质量通过大活塞又给了小活塞感到困惑、十分不解。对于这种准双作用式或者就是双作用式活塞,描述的位移公式形式上有两种,经求导后得出的加速度公式也有两种,然而形成的惯性力表现形式仅有一种,正好等同于传统的单作用式的那种,这些都是经过严密推导出来的,不是主观臆测的。科学是十分奇妙的,讲究对称与严谨,当你深入下去就会探索到“山穷水复疑无路,柳暗花明又一村”的境界。将轴侧加速度图与盖侧加速度图相对照,轴侧180°开始后再添个负号,就是盖侧的加速度线。
压缩机教材上指出,实际上制作惯性力曲线时,是直接作在各列气体力曲线一起的,以便与摩擦力一道叠加成活塞力曲线。根据动力计算程序得出,具有观点四形成的惯性力曲线与观点一、二、三相比较,合成后的总活塞力的72组数据中的最大值居最小,虽然各自相差不多。
点评:以上四种观点层层推进,步步为营,最终得出了观点四的正确结论。观点一抓大放小,它与观点四在各个位置时力的分析都是相差最小的,虽然看起来有些粗糙;观点二的毛病,从后面来看是没有考虑到轴侧活塞的惯性力对连杆的作用受压还是受拉,即观点二式i后是以“-”来连接,同时重复计及十字头等往复质量,所以不对;观点三认同两质量相等是一大进步,若 、取两项相加就多算了一份;观点四是正确的结论,它是观点一、二、三的完美概括。
、取两项相加就多算了一份;观点四是正确的结论,它是观点一、二、三的完美概括。
4、准双作用活塞组件θ=45°时受力分析
最后以统一坐标系中,θ约45°分析一下活塞的受力,见图4。
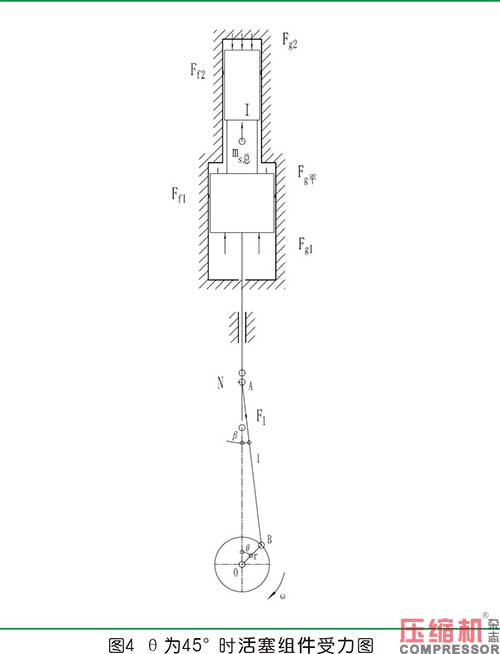
说明一下,fg1、fg2、fg平、ff1、ff2、i、n、fl组成一组平衡力系,图中每一种力的箭头标示了该状态下的方向。用fp表示活塞力,则其表达式为:
参考文献
(1)陈永江,容积式压缩机原理与结构设计,[m],西安交通大学出版,1985
(2)林梅,孙嗣莹,活塞式压缩机原理,[m],西安交通大学,2006
(3)陆鹏程,张光胜,三星型压缩机振动问题研究,[j],安徽工程科技学院学报,2009.1:62-65
(4)侯宝安,关于惯性力的看法,[j],山东建材学院学报,1987.1
(5)张玉良,上海化学工业专科学校,惯性力辨析,化工装备技术,1989.10
来源:本站原创
【】在2023年10月刊《准双作用式理论问题研究》一文中,笔者推导了准双作用式的活塞位移公式,介绍了其在压缩机研究、设计中的应用,并提到了压缩机动力计算。本文在探讨压缩机动力计算程序之前,先具体谈谈构成压缩机活塞力成分之一——惯性力的问题。
1、惯性力概念发展简史
先简单谈谈传统的手工绘制动力曲线的计算方法。构成列的活塞力由气体力、惯性力、摩擦力三部分相加之和而形成。列的气体力图采用勃劳厄(brauer)法绘制;列的惯性力图通常采用托尔(tolle)法绘制,近似地绘制出一阶、二阶惯性力之和;列的摩擦力图是按经验法绘制,通常的做法是在向轴行程中认为是一不变的正值,而在向盖行程中则认为是一负的不变的值,在内、外止点时作一斜线修正。它的作用方向始终与活塞运动速度方向相反。这三种方法绘制的各自力图中,都面临着横坐标的转换,因为活塞式压缩机是曲柄连杆机构,将主运动的旋转运动通过连杆转换成活塞的上、下往复运动。各自的力图一般先采用“力-位移”坐标系,它们都是周期性的,主曲柄旋转一周360°时,活塞则经“外止点-内止点-外止点”这样一个循环。而列的活塞力图一般采用“力-曲柄转角”坐标系构成,包括后来的列的切向力图、列的法向力图、列的连杆力图、列的侧向力图,都是采用这样的坐标系来分析。所以说,对于横坐标由行程转化为曲柄旋转角的问题,教材上都给出了采用勃力克斯(brix)近似作图法,并给予了相应证明,这里不作展开论述。这就是传统的手工作图方法,而现在则直接采用经推导的公式将三种力图直接绘制成“力-曲柄转角”坐标系中。不过有些细节仍是近似的。例如,气体力经气的作用,在转折点处没有考虑现实中的脉动状态,惯性力图也仅考虑了一、二阶,对其后的三阶等没有考虑,而摩擦力图是最简单的简化过程,并且统计出的机械效率具体值也是一个经验值。虽然是这样但这些简化也是我们动力计算时作出的正确抉择。
惯性力是什么?历史上关于惯性力的争论由来已久,可追溯到三百年前左右。惯性力就是按达朗伯原理,将动力学问题转化成静力学问题的一种研究方法。这种力比较特殊,它没有明确的力的三要素概念,所以有些人认为是虚拟的,它实际上是以“-ma”形式出现。而更多的学者坚持认为它是一种真实的力,不然就无法解释高速旋转的机器,例如航空燃气涡轮叶片根部断裂现象。这些在压缩机上也有类似的现象,归根到底都是实际物体的内力与外力、相对与绝对的问题。
2、压缩机中惯性力的大小
据作者统计,在各种型式的压缩机中,构成某一列的活塞运动组件,其该列受到的往复惯性力的幅值占该列所受到的气体力的幅值百分比,约为7~40%,这是作者不完全的统计。它基于作者目前所了解到的各种国内的压缩机经作者近似比算的,实际反映了各型的设计者对惯性力的认识作出的设计。请读者应该注意的是,这里的活塞包括单作用式、双作用式的,而这里的惯性力的演算方法则是该篇文章所详细讨论的内容。

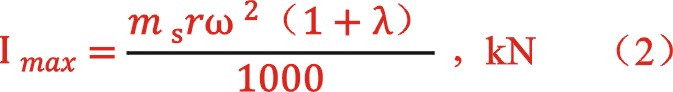
其中:imax——列的最大往复惯性力
ms——盖侧往复质量,包括盖侧活塞、环、活塞杆、十字头体、销、连杆重心偏向于小头部分的连杆质量(约占连杆总质量的30~40%),kg。轴侧质量待后面讨论
r——曲柄半径,m
ω——曲柄旋转角速度,1/s,,n为机器转速,r/min
λ——曲柄半径连杆中心距之比,,为连杆中心距长度

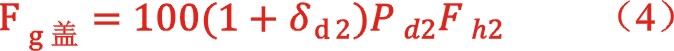
其中:δd2——准双作用式盖侧容积腔部分的排气时相对压力损失
pd2——准双作用式盖侧容积腔部分的名义的排气绝对压力,bar
fh2——该容积腔所作用的活塞面积,m2,

代表盖侧气缸直径

其中:p平——指平衡腔的压力,bar,它与机器的运动机构利用系数μ有关。一般接一级排压力腔,它可以减轻高压缸活塞环工作负荷,避免向低压级腔泄漏,这里计算b值时不考虑。
fh气缸圆环——指下面的大气缸与上面的小气缸工作面积差,m2
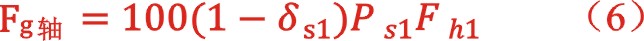
其中:δs1——准双作用式轴侧容积腔部分的吸气时相对压力损失
ps1——准双作用式轴侧容积腔部分的名义的吸气绝对压力,bar
fh1——该容积腔所作用的活塞面积,m2,
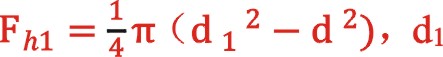
代表轴侧气缸直径,d代表活塞杆直径
pgas——列的最大气体力,它一般指的是盖侧活塞θ=0而轴侧活塞处在θ=π时的状态
b——惯性力的幅值与气体力的幅值的百分比,%
3、关于惯性力在准双作用式压缩机中表现形式的几种思考
大家知道,在曲柄连杆机构中,列的往复惯性力i为:
注意,它通常指的是盖侧活塞的惯性力。相信大部分读者可能都比较迷惑,为什么刚开始作惯性力图时,在外止点即θ=0时,将作在正力方向时,就能将上式“-”取消?这是因为,在盖侧活塞工作过程中,θ=0°开始后,位移由0渐变正(方向向下),速度也是由0渐变正(方向向下),而加速度则是由正的最大值渐变小(引起的速度还是渐变大),其方向也是向下,加个负号则方向变上,则此时该力的作用使连杆受拉,故手工作图时作在正力方向上,已考虑了“-”。
同理,θ=180°时,,该值为负,作在“力-曲柄转角”坐标系下方。
下面以具有图1形式的准双作用式压缩机某一列为算例,详尽讨论对变值的惯性力计算的思考。

已知:活塞组件质量7.8kg(其上小活塞3.2kg,下面大活塞4.6kg)
环0.6kg
活塞杆8.2kg
十字头10kg
销1.4kg
连杆小头4kg
综上,运动部件总质量32kg,其中盖侧运动部件总质量27.4kg,轴侧运动部件总质量28.8kg
曲柄旋转半径

角速度
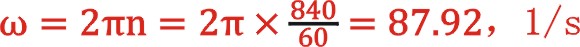
曲柄半径连杆比
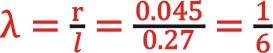
观点一:仅考虑了盖侧活塞组件的质量
由(7)式得到:
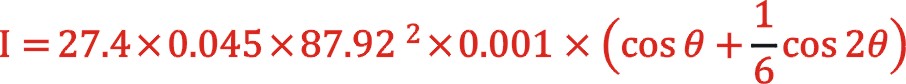
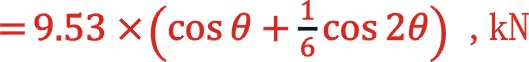
由此得到惯性力的最大值与最小值为11.13,-7.95kn。以该数系同气体力、摩擦力参与了该列活塞力的演算,忽略了轴侧大活塞的影响,可能当时还没有意识到轴侧惯性力如何计算。
观点二:因为按照动力的传递,由连杆小头带动十字头、活塞杆,进而大活塞、小活塞,作上下往复运动,认为:


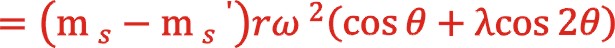
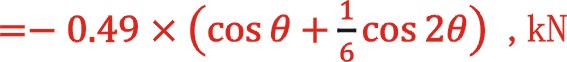
由此得到惯性力的最大值与最小值为0.41,-0.57kn。其中第二项是这样演算的:当将内止点选做坐标系的原点,向上为正方向,以轴侧活塞开始膨胀点为起始点后,其:
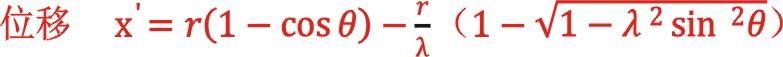

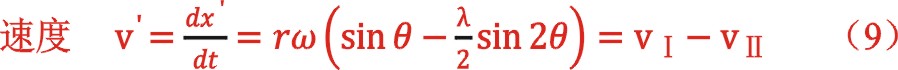
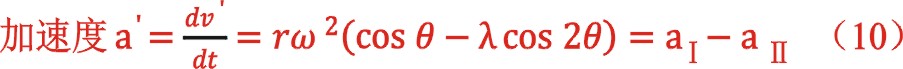
当盖侧与轴侧都统一到盖侧的外止点处一套坐标系后,也考虑到初始时各自的正负值后,总的惯性力应是盖侧的惯性力与式(10)的之和(不过后来发现还是不对),大家可能发现盖侧与轴侧往复质量中将连杆小头、十字头、活塞杆质量计及了两次,算出的参与计算的质量仅是大、小活塞质量的差值,这不知有没有道理?不过我们或许都知道,惯性力在机器运转过程中,不参与做功,不影响最终平均切向力的大小,仅影响活塞力和平均切向力的具体形状,影响机器曲轴的静强度计算,并且其幅值相对气体力来说较小。
观点三:由观点二得出推论, 、计入可能有误,应该是
、计入可能有误,应该是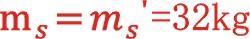 ,所以。
,所以。
观点四:不论以盖侧活塞计算惯性力的变化曲线,还是以轴侧活塞来计算,其计算结果都是一样的,即以观点一中的公式来计算,式中ms=32kg,证明如下:

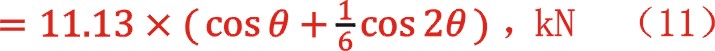
由此得到惯性力的最大值与最小值为13,-9.29kn。
根据盖侧的位移、速度、加速度图解,见图2。



据轴侧的位移、速度、加速度图解,见图3。它就是按式(8)、(9)、(10)分两部分叠加而成。



轴侧0°时,位移为正(方向向上),速度为正(向上),加速度为正(向上),-ma向下,连杆受压,作在负值(-1+λ)处;轴侧180°时,位移为正的最大值,速度为0渐变负(向下),加速度为负的最大值(向下),-ma向上,连杆受拉,作在正值(1+λ)处。
由此可见,形式上具有图1中的大活塞进行的轴侧加速度的变化,其受力分析表明,在统一的一套坐标系中θ=0时,将惯性力的起始点作在正的(1+λ)为力的系数处,参与的质量是全部的往复运动质量,这正好与普通盖侧惯性力曲线起始点作图一致。这很好地解决了观点二和观点三中十字头等处质量参与计算两次的问题,当时也因为这一处质量通过大活塞又给了小活塞感到困惑、十分不解。对于这种准双作用式或者就是双作用式活塞,描述的位移公式形式上有两种,经求导后得出的加速度公式也有两种,然而形成的惯性力表现形式仅有一种,正好等同于传统的单作用式的那种,这些都是经过严密推导出来的,不是主观臆测的。科学是十分奇妙的,讲究对称与严谨,当你深入下去就会探索到“山穷水复疑无路,柳暗花明又一村”的境界。将轴侧加速度图与盖侧加速度图相对照,轴侧180°开始后再添个负号,就是盖侧的加速度线。
压缩机教材上指出,实际上制作惯性力曲线时,是直接作在各列气体力曲线一起的,以便与摩擦力一道叠加成活塞力曲线。根据动力计算程序得出,具有观点四形成的惯性力曲线与观点一、二、三相比较,合成后的总活塞力的72组数据中的最大值居最小,虽然各自相差不多。
点评:以上四种观点层层推进,步步为营,最终得出了观点四的正确结论。观点一抓大放小,它与观点四在各个位置时力的分析都是相差最小的,虽然看起来有些粗糙;观点二的毛病,从后面来看是没有考虑到轴侧活塞的惯性力对连杆的作用受压还是受拉,即观点二式i后是以“-”来连接,同时重复计及十字头等往复质量,所以不对;观点三认同两质量相等是一大进步,若 、取两项相加就多算了一份;观点四是正确的结论,它是观点一、二、三的完美概括。
、取两项相加就多算了一份;观点四是正确的结论,它是观点一、二、三的完美概括。
4、准双作用活塞组件θ=45°时受力分析
最后以统一坐标系中,θ约45°分析一下活塞的受力,见图4。

说明一下,fg1、fg2、fg平、ff1、ff2、i、n、fl组成一组平衡力系,图中每一种力的箭头标示了该状态下的方向。用fp表示活塞力,则其表达式为:
参考文献
(1)陈永江,容积式压缩机原理与结构设计,[m],西安交通大学出版,1985
(2)林梅,孙嗣莹,活塞式压缩机原理,[m],西安交通大学,2006
(3)陆鹏程,张光胜,三星型压缩机振动问题研究,[j],安徽工程科技学院学报,2009.1:62-65
(4)侯宝安,关于惯性力的看法,[j],山东建材学院学报,1987.1
(5)张玉良,上海化学工业专科学校,惯性力辨析,化工装备技术,1989.10
来源:本站原创
网友评论
条评论
最新评论